水平線と地平線は大体4km先でしかない

遮蔽物がない遠くを見渡せる場所で果てを見ると、地平線や水平線を見ることができます。 こういった景色を見ると「あそこには何があるんだろう」と考えさせられますよね。
でも水平線や地平線って、大体4~5km先なんですよ。 水平線はともかく地平線に何があるかは1時間もあれば確認できるんですよね。
水平線・地平線までの距離の計算方法
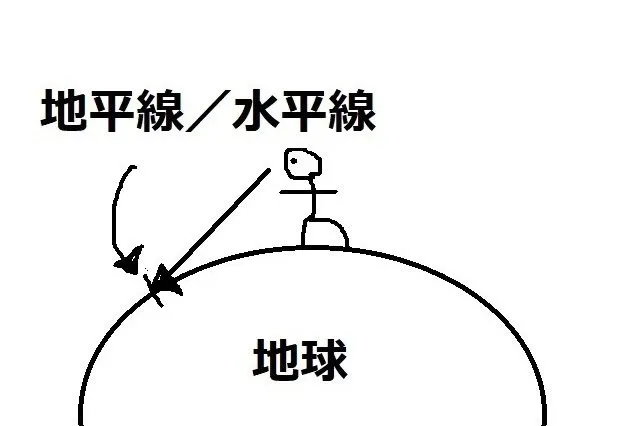
言うまでもなく地球は丸いです。なのでどこまでも先を見通すことはできません。 どこまで先を見渡せるかは目線の高さによって変わり、目線が高ければそれだけ水平線・地平線も先の景色になりますし、その逆も然りです。
どこまで先が見えるかは三平方の定理によって算出できます。 公式は以下の通りです。
惑星上で見通せる距離の公式
√(2*天体の半径*目線の高さ)
地球の半径はおよそ6370kmです。 目線の高さを170cmとした場合、地/水平線の距離の計算は以下のようになります。
地球上で見通せる距離の計算式
√(2*6370*0.0017)≒4.65km
という訳で170cmの高さから見た場合の水平線・地平線はおよそ4.65km先になります。 折角なので色々な高さを当てはめてみると、以下のようになります。
| 目線の高さ | 水平線・地平線の距離 |
|---|---|
| 8000m(エベレスト級) | 451km |
| 3000m(富士山級) | 195km |
| 2000m | 159km |
| 1000m | 113km |
| 634m(スカイツリー) | 89km |
| 333m(東京タワー) | 65.1m |
| 170cm | 4.65km |
| 150cm | 4.38km |
| 30cm | 1.95km |
山の頂上や高い建物から果てを眺める場合、今いる標高から計算してどの辺りまで見えているのかを考えてみるのも面白いかもしれませんね。
なお月のように小さい天体においては地平線までの距離が短くなり、木星のような大きい天体においては地平線までの距離が長くなります。170cmの人ベースで考えた場合、地球では4.65km先だった地平線が月では2.43km先、木星では142km先となります。
地球がまるいから水平線や地平線が存在する
遠くへ行く船を陸から眺めていると、だんだんと沈んでいってやがて水平線の先に沈んでいきます。実はこれ地球が丸いからなんです。
もしも地球が平面だった場合、遠くへ行くほど小さくなりますが沈んで見えなくはなりません。 今よりもずっと先の景色まで見渡せることでしょう。
水平線の先から近づいてくる船は穂先、マスト、船全体という順で現れます。 地球がまだ平面だと信じられていた頃にも、これを見た船乗りたちは「もしかすると地球は丸いんじゃないか」と考えていたそうですよ。
また地球が丸いと分かった後にも、それを知らない・信じない人への説明のために水平線の例はよく使われていました。今でも学校などで聞くことがあるのではないでしょうか。
水平線は地球においてはたかが4km先ですが、そこには色々な浪漫が詰まっているのです。







